2. Describing Data with Tables and Graphs
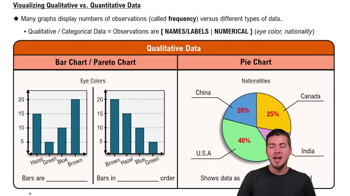
Visualizing Qualitative vs. Quantitative Data
2:28 minutesProblem 12.CRE.8
Textbook Question
Win 4 Lottery Shown below is a histogram of digits selected in California’s Win 4 lottery. Each drawing involves the random selection (with replacement) of four digits between 0 and 9 inclusive.
b. Does the display depict a normal distribution? Why or why not? What should be the shape of the histogram?
Verified step by step guidance1
Observe the histogram provided. A normal distribution is characterized by a symmetric, bell-shaped curve where most of the data is concentrated around the mean, and the frequencies taper off equally on both sides.
Analyze the shape of the histogram. In this case, the frequencies of the digits are not symmetric. For example, digits like 6 and 7 have very low frequencies compared to others, and there are peaks at digits like 2, 5, 8, and 9.
Conclude that the histogram does not depict a normal distribution because it lacks symmetry and the bell-shaped curve. Instead, the distribution appears irregular with multiple peaks and valleys.
Consider what the shape of the histogram should be. Since the lottery involves random selection with replacement, each digit (0 through 9) should theoretically have an equal probability of being selected. This would result in a uniform distribution where all bars in the histogram are approximately the same height.
Summarize that the observed histogram deviates from the expected uniform distribution, suggesting potential irregularities or biases in the digit selection process.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Normal Distribution
A normal distribution is a symmetric, bell-shaped distribution characterized by its mean and standard deviation. In a normal distribution, most of the data points cluster around the mean, with fewer points appearing as you move away from the mean. This distribution is important in statistics because many statistical tests assume normality in the data.
Recommended video:
Guided course
09:47
Finding Standard Normal Probabilities using z-Table
Histogram
A histogram is a graphical representation of the distribution of numerical data, where the data is divided into bins or intervals. The height of each bar indicates the frequency of data points within that interval. Histograms are useful for visualizing the shape of the data distribution, including its central tendency and variability.
Recommended video:
Guided course
05:54Intro to Histograms
Random Sampling
Random sampling is a technique used to select a subset of individuals from a larger population, where each individual has an equal chance of being chosen. In the context of the lottery, random sampling ensures that each digit has an equal probability of being drawn, which is essential for the fairness and unpredictability of the lottery results.
Recommended video:
05:11Sampling Distribution of Sample Proportion
4:39mWatch next
Master Visualizing Qualitative vs. Quantitative Data with a bite sized video explanation from Patrick
Start learning
