In Exercises 5–8, answer the questions by referring to the fol...

Question

In Exercises 5–8, answer the questions by referring to the following Minitab-generated histogram, which depicts the weights (grams) of all quarters listed in Data Set 40 “Coin Weights” in Appendix B. (Grams are actually units of mass and the values shown on the horizontal scale are rounded.)

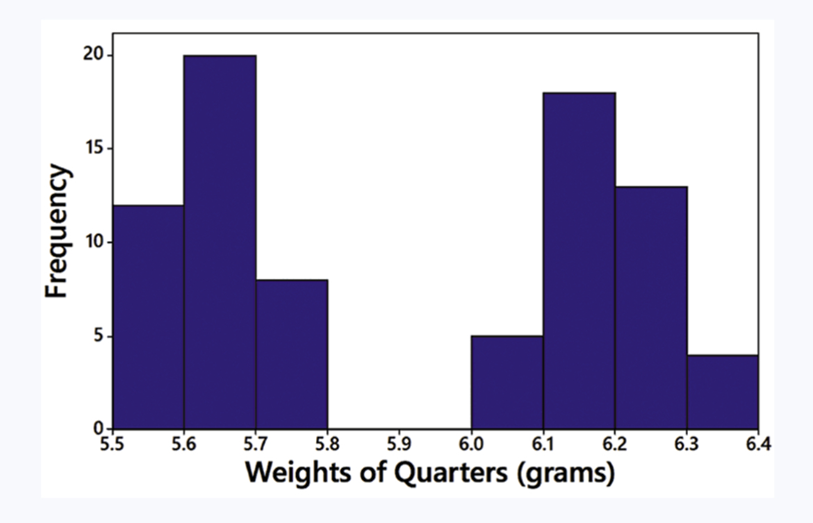
Histogram showing the frequency of quarter weights in grams, with bars representing weight ranges from 5.5 to 6.4 grams.

Relative Frequency Histogram How would the shape of the histogram change if the vertical scale uses relative frequencies expressed in percentages instead of the actual frequency counts as shown here?

Accepted Answer

Hello, everyone. Let's take a look at this question together. Use the following histogram generated by statistical software, which represents the battery life in hours of a sample of smartphones. Note that the values on the horizontal scale are. Rounded. How would the shape of the histogram be affected if the vertical axis displayed relative frequencies in percentages instead of actual frequency counts? And here we have our histogram of smartphone battery life. Is it answer choice A, the shape of the histogram would change significantly with taller bars becoming shorter and shorter bars becoming taller? Answer choice B, the shape of the histogram would remain the same, but the vertical axis would show percentages instead of actual frequencies. Answer choice C, the histogram would become skewed because percentages are used instead of counts, or answer choice D, the distribution would become uniform. With all bars having equal height. So, in order to solve this question, we have to recall what we have learned about the shape of a histogram to determine how it would be affected if the vertical axis displayed relative frequencies in percentages instead of actual frequency counts. Well, we know that relative frequency histograms and frequency histograms have identical shapes, which they have identical shapes because the proportions between bars remain unchanged, and the only difference is the scaling of the vertical axis, since instead of showing counts, It would show percentages of the total sample. Therefore, if the vertical axis of the histogram displayed relative frequencies in percentages instead of actual frequency counts, the relative heights of the bars would stay the same, ensuring that the distribution pattern remains on its. Changed. So looking at our answer choices, we can identify that answer choice B is the correct answer. As answer choice B says, the shape of the histogram would remain the same, but the vertical axis would show percentages instead of actual frequencies. So answer choice B is the correct answer, and all other answer choices are incorrect. I hope you found this video to be helpful. Thank you and goodbye.

��app

Key Concepts

Histogram

Relative Frequency

Shape of the Histogram

Watch next