81. Genetics A Punnett square is a diagram that shows all poss...

Question

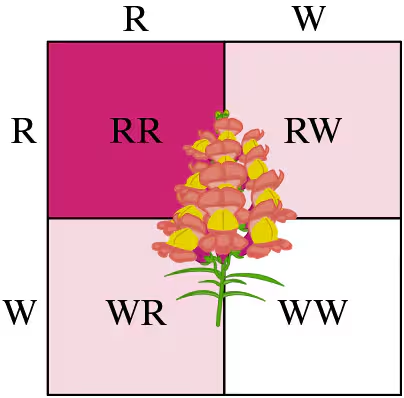
81. Genetics A Punnett square is a diagram that shows all possible gene combinations in a cross of parents whose genes are known. When two pink snapdragon flowers (RW) are crossed, there are four equally likely possible outcomes for the genetic makeup of the offspring: red (RR), pink (RW), pink (WR), and white (WW), as shown in the Punnett square at the left. When two pink snapdragons are crossed, what is the probability that the offspring will be (c) white?

Punnett square showing gene combinations for pink snapdragons, with outcomes: red (RR), pink (RW, WR), and white (WW).

Accepted Answer

Hi everyone, let's take a look at this practice problem. This problem says in rabbits, fur collar is determined by a single gene with two alleles, B for black and W for white. The black fur allele, B is dominant, and the white fur allele W is recessive. When two heterozygous black rabbits, BW, are crossed, the offspring can have the following genetic combinations BB, which gives black fur, BW, which gives black fur, WB, which gives black fur, and WW, which gives white fur. When two heterozygous black rabbits are crossed, what is the probability that the offspring will be white? And we have 4 possible choices as our answers. For choice A, we have 1 divided by 4, for choice B, we have 1 divided by 2. For choice C, we have 3 divided by 4, and for choice D, we have 1. So we're asked to find the probability that the offspring will be white when two heterozygous black rabbits are crossed, and we're told in the problem that there are 4 possible outcomes. And that those outcomes are BB, which will be black fur, BW, which will be black fur, WB which will give black fur, and WW which will give white fur. So only 1 out of the 4 possible outcomes give white fur. So now we need to use this information to construct a probability, which we'll call the. We call that a probability is going to be equal to the number of favorable outcomes divided by the total number of possible outcomes. So in this case, we only have one favorable outcome, so we'll have 1, and we're dividing that by the 4 possible outcomes. So we'll have 1 divided by 4 for our probability. And so that is the answer that we're looking for for this problem. And if we compare that to our answer choices, we see that the correct answer choice corresponds to answer choice A. So, I hope that this explanation has been useful, and I'll see you in the next video.

��app

Watch next

����app

Watch next

��app