Graphical Analysis In Exercises 11–16, determine whether the g...

Question

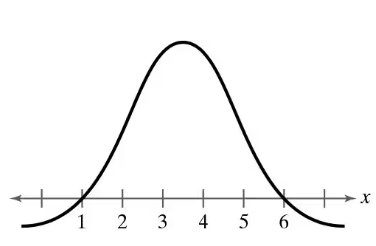
Graphical Analysis In Exercises 11–16, determine whether the graph could represent a variable with a normal distribution. Explain your reasoning. If the graph appears to represent a normal distribution, estimate the mean and standard deviation.

dist2

Accepted Answer

Hello there. Today we're going to solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. Could this graph represent a variable with a normal distribution? If so, estimate the mean and standard deviation. If not, explain your reasoning. Awesome. So it appears for this particular problem we're asked to take our graph that is provided to us, and we're asked to determine if this graph could represent a variable with a normal distribution, and if it does represent a variable with a normal distribution. We're asked to estimate what the mean and standard deviation will be, and if it is not a variable with normal distribution, we're asked to explain why it is not a variable with normal distribution. So with that in mind, now that we know what we're ultimately trying to solve for, let's look at our graph. As you can see, we have a curve represented in blue, and as you can see, it crosses the x axis at 10 and 15. And it also has a peak at about roughly 12.5. We can also note and recall that just by looking at our graph visually, the curve appears to be symmetric and bell shaped. However, it's important to note, as we should recall, that a normal curve should approach but never touch the x axis as it extends farther from the mean. So in our provided graph, we could see very clearly that the curve crosses the X axis at both ends. Which implies, as we should recall, that a probability can be negative, 0, or positive. And for a variable to have a normal distribution. Its density curve must always be above the X axis for all real values of X. So, mathematically, the normal distribution's probability density function is always positive, as we should recall, it states that F of X is equal to 1 divided by sigma multiplied by the square root of 2 multiplied by pi. All multiplied by E to the power of negative X minus m to the power of 2 divided by 2 multiplied by sigma to the power of 2. Fantastic. And we need to note that the denominator, which is 2 multiplied by the square root of 2 multiplied by pi, is always positive because sigma, the standard deviation, must be a value greater than 0, and we also need to note and recall that the exponential part will always be positive. And the numerator one is always positive and is a constant value. So therefore, with that in mind, the curve does not represent a variable with a normal distribution because it crosses the X axis. So therefore, our final answer without a doubt has to be no because the curve crosses the x axis. And that's it. We've officially solved for this problem. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

��app