6. Normal Distribution and Continuous Random Variables
Standard Normal Distribution
1:48 minutesProblem 5.1.17
Textbook Question
Using and Interpreting Concepts
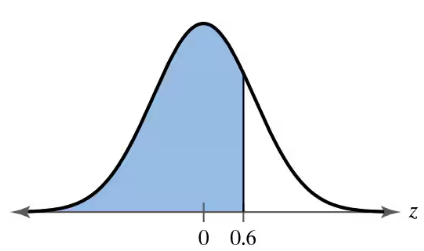
Finding Area In Exercises 17–22, find the area of the shaded region under the standard normal curve. If convenient, use technology to find the area.
Verified step by step guidance1
Step 1: Understand the problem. The goal is to find the area of the shaded region under the standard normal curve. The shaded region represents the cumulative probability from z = -∞ to z = 0.6.
Step 2: Recall that the standard normal curve is symmetric about z = 0, and the total area under the curve is 1. The area to the left of z = 0.6 can be found using the cumulative distribution function (CDF) of the standard normal distribution.
Step 3: Use the z-score table or technology (such as a graphing calculator or statistical software) to find the cumulative probability corresponding to z = 0.6. This value represents the area under the curve to the left of z = 0.6.
Step 4: If using a z-score table, locate the row corresponding to z = 0.6. The table will provide the cumulative probability for this z-score. If using technology, input the z-score into the software's standard normal CDF function.
Step 5: Interpret the result. The cumulative probability obtained represents the proportion of the distribution that lies to the left of z = 0.6, which is the area of the shaded region.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Normal Distribution
The standard normal distribution is a special case of the normal distribution where the mean is 0 and the standard deviation is 1. It is represented by the bell-shaped curve, and all values are expressed in terms of z-scores, which indicate how many standard deviations an element is from the mean. This distribution is crucial for statistical analysis, particularly in hypothesis testing and confidence intervals.
Recommended video:
Guided course
09:47
Finding Standard Normal Probabilities using z-Table
Z-Score
A z-score is a statistical measurement that describes a value's relationship to the mean of a group of values. It is calculated by subtracting the mean from the value and then dividing by the standard deviation. Z-scores are essential for determining the position of a data point within a standard normal distribution, allowing for the comparison of scores from different distributions.
Recommended video:
Guided course
06:31Z-Scores From Given Probability - TI-84 (CE) Calculator
Area Under the Curve
In the context of the normal distribution, the area under the curve represents the probability of a random variable falling within a particular range. The total area under the curve is equal to 1, and specific areas can be calculated using z-scores and standard normal distribution tables or technology. This concept is fundamental for understanding probabilities and making inferences about populations based on sample data.
Recommended video:
Guided course
08:50Z-Scores from Probabilities
9:47mWatch next
Master Finding Standard Normal Probabilities using z-Table with a bite sized video explanation from Patrick
Start learning