In Exercises 1–5, use the data listed in the margin, which are...

Question

In Exercises 1–5, use the data listed in the margin, which are magnitudes (Richter scale) and depths (km) of earthquakes from Data Set 24 “Earthquakes” in Appendix B

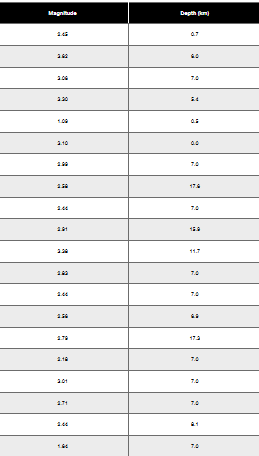
Table displaying data with two columns: Magnitude and Depth, listing various values for each category.

Histogram Construct the histogram corresponding to the frequency distribution from Exercise 1. For the values on the horizontal axis, use the class midpoint values. Which of the following comes closest to describing the distribution: uniform, normal, skewed left, skewed right?

Accepted Answer

Hi, everyone, let's take a look at this practice problem. This problem says the following frequency distribution represents the delivery time in minutes for packages shipped from a logistics center, and we're given a table that has in the first column, the delivery time in minutes, and it has the intervals of 10 to 1920 to 29, 30 to 39, 40 to 49, and 50 to 59. In the next column, we have our frequency, and it has the values of 47, 12, 8, and 3. Construct a histogram corresponding to this frequency distribution. Which of these best describes the distribution? Uniform, normal, skewed left, or skewed, right? So, the first thing we need to do is to create a histogram. And to do this, we're actually going to create the, we're actually going to calculate the midpoint of each of our delivery time intervals. And we call it to calculate a midpoint. That that is going to be equal to. The upper bound, which we'll label as UB. Plus the lower bound, which we'll label as LB. And then that quantity is going to be divided by 2. So, we're actually going to create a third column in our table called midpoint. And we're gonna calculate the midpoint for each of our delivery time intervals. So, for the interval between 10 minutes and 19 minutes, calculating its midpoint, we get 14.5. 4 22 29. We get a midpoint of 24.5. 4:30 to 39, the midpoint is going to be 34.5. From 40 to 49, the midpoint is going to be 44.5. And then finally, from 50 to 55 minutes, the midpoint is going to be 54.5. So now we're going to use our midpoints and frequencies to create a histogram. So to construct a histogram, we can either use a spreadsheet software program or manually draw it on graph paper. But in either case, on the x-axis, we're going to plot our class midpoints and on the y axis, we're going to plot the corresponding frequencies, and we're actually going to draw vertical bars with heights equal to the frequency for each class. So doing so, we get the following graph. We're on the x axis, we have our midpoints for our class intervals, and that's going to be the 14.5, 24.5, 34.5, 44.5, and 54.5. And for each of those midpoints, we have drawn a vertical bar to the height corresponding to the frequencies. And so for 14.5, we have a frequency of 4, for 24.5 we have frequency of 7. For 34.5, we have a frequency of 12. For 44.5 we have frequency of 8, and for 54.5, we have a frequency of 3. So this here is the histogram that the problem was looking for. So now we need to answer the second half of this question, which is which of these best describes the distribution, uniform, normal, skewed left or skewed right. So we need to recall the definition of each of these distributions. So recall for the uniform distribution that the frequencies should be approximately equal across all classes. For a normal distribution, the histograms should be unimodal, symmetric, and bell-shaped. For skewed left, the left tail is longer, meaning high more high values with fewer low values. And for skewed right, the the right tail is longer, meaning more low values with fewer high values. And if we look at our histogram, we see that it has a peak near the center of 34.5, and gradually decreases towards both tails, and the distribution appears roughly normal. So that means that the answer to the second half of this question is normal. So I hope that this explanation has been useful, and I'll see you in the next video.

��app

Key Concepts

Histogram

Class Midpoint

Distribution Shape

Watch next