6. Normal Distribution and Continuous Random Variables
Probabilities & Z-Scores w/ Graphing Calculator
2:20 minutesProblem 6.1.7
Textbook Question
Continuous Uniform Distribution. In Exercises 5–8, refer to the continuous uniform distribution depicted in Figure 6-2 and described in Example 1. Assume that a passenger is randomly selected, and find the probability that the waiting time is within the given range.
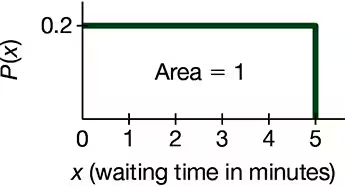
Between 2 minutes and 3 minutes
Verified step by step guidance1
Step 1: Recognize that the problem involves a continuous uniform distribution. The graph provided shows a uniform distribution where the probability density function (PDF) is constant at P(x) = 0.2 over the interval [0, 5]. The total area under the curve is 1, as required for a probability distribution.
Step 2: Recall the formula for the probability in a continuous uniform distribution. The probability of a random variable falling within a specific range [a, b] is given by: P(a ≤ X ≤ b) = (b - a) * f(x), where f(x) is the constant height of the PDF.
Step 3: Identify the range of interest. The problem asks for the probability that the waiting time is between 2 minutes and 3 minutes. Here, a = 2 and b = 3.
Step 4: Substitute the values into the formula. Use f(x) = 0.2 (from the graph) and calculate the width of the interval (b - a), which is (3 - 2). The formula becomes: P(2 ≤ X ≤ 3) = (3 - 2) * 0.2.
Step 5: Simplify the expression to find the probability. Multiply the width of the interval by the height of the PDF to determine the probability. This will give you the final result.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
7:09mWatch next
Master Probability From Given Z-Scores - TI-84 (CE) Calculator with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
