In Exercises 9–20, use the data in the following table, which ...

Question

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

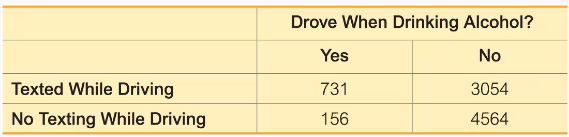
Survey table of high school drivers: texting vs. drinking and driving behavior.

Texting and Alcohol If three of the high school drivers are randomly selected from the 4720 subjects who did not text while driving, find the probability that all three drove when drinking.

a. Assume that the selections are made with replacement. Are the events independent?

Accepted Answer

Hi, everyone. Let's take a look at this practice problem. This problem says a study on screen habits and sleep patterns collected survey results from high school students aged 16 and older. The table below summarizes responses based on whether students used electronic devices right before bed and whether they reported poor sleep quality. And below the text we're given a table where one row is labeled use electronic devices before bed. And the next two columns are for reported poor sleep, and the first column, we have yes, and it has value of 820. And for the next column, we have no, and it has a value of 2940. The next row is labeled as did not use electronic devices, and under the poor sleep columns, we have for yes, we have a value of 210, and for no, we have 40,030. Find the probability that all 3 students reported poor sleep, given that they are selected from the group that did not use devices before bed. Assume that these selections are made with replacement. Are the events independent? So, the first thing we need to do is find the probability that all 3 of our selected students reported poor sleep, assuming that the selections are made with replacements. So, in order to do that, we need to find the total number of students surveyed that did not use electronic devices. So we'll call that value in. And this is just going to be equal to from our table 210 plus 40,030. And when we add these two values together, we'll get 4240. So now we need to calculate the probability that all 3 students that are selected reported poor sleep out of this group. And we're gonna start off by calculating the probability that just 1 student selected reports poor sleep. So we'll call that probability P1, and recall that a probability is going to be equal to the total number of favorable outcomes divided by the total number of possible outcomes. So, the number of favorable outcomes in this case is going to be 210, since that's the number of students that reported poor sleep and did not use electronic devices before bed. And that's going to be divided by the total number of possible outcomes, which we just calculated of 4240. And simplifying this fraction, this is going to be equal to 21 divided by 424. So now, we can calculate the probability that all 3 students selected reported poor sleep. So we'll call this probability P3. And since we're um making the selections with replacement, that means that P3 here is just going to be equal to the probability P1 cubed. Since each selection of a student will bring in a factor of P1. And so this is going to be equal to the quantity of 21 divided by 424 in quantity cut. And this is going to be approximately equal to 0.00012. So this here is the probability that we're looking for for this problem. So now we need to determine whether our events here are independent or not. And since these selections are being made with replacement, that means that the selection of one of the students is not, does not affect the selection of the other two, since the selected student goes back into the poor students to be selected again. So since the selections do not affect one another, that means that our events are independent. So the answer to the second half of this question is yes, the events are independent. So these are the answers for this problem. So I hope that this explanation has been useful, and I'll see you in the next video.

��app

Key Concepts

Probability

Independent Events

Sampling with Replacement

Watch next