In Exercises 9–20, use the data in the following table, which ...

Question

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

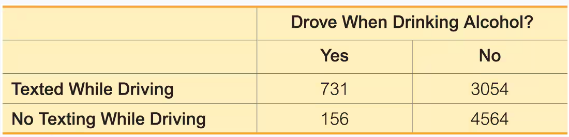
Texting and Alcohol If one of the high school drivers is randomly selected, find the probability that the selected driver did not text while driving and did not drive when drinking.

Survey table of high school drivers: texting and driving vs. drinking and driving, with numerical data.

Texting and Alcohol If one of the high school drivers is randomly selected, find the probability that the selected driver did not text while driving and did not drive when drinking.

Accepted Answer

Welcome back, everyone. A study on screen habits and sleep patterns collected survey results from high school students aged 16 and older. The table below summarizes responses based on whether students used electronic devices right before bed and whether they reported poor sleep quality. If one high school student is randomly selected, find the probability that the selected student did not use electronic devices before bed and did not report or sleep. For this problem we want to identify the probability, right? We're going to label our event A, and that event represents that the selected student did not use electronic devices before bed and did not report for sleep. Now how do we find probability? Well, it is the ratio between two numbers M and N. Where M is the number of favorable outcomes. And N is the total number of outcomes. Let's begin with the total. So we have a study and our total essentially represents all of the participants in the study. So we have to sum all the 4 numbers given to us. N is 820. Plus 2940. + 210 + 40,030. And this gives us 8000 participants, right? So our denominator is 8000. And now we have to identify the number of favorable outcomes. Those are the students who did not use electronic devices. So we're looking at the final row. It says did not use electronic devices. Before bed and did not report where sleep so we're looking at the final row which says no or reported poor sleep question mark right so the intersection between those. Provides us with 4000. 30 students. Well, once we have our M and N values, we have to perform division, and we can now get the final answer, which is 0.50375. That would be our final answer for this problem. Thank you for watching.

��app

Key Concepts

Probability

Contingency Table

Complementary Events

Watch next