Testing for Rank Correlation
In Exercises 7–12, use the ...

Question

Testing for Rank Correlation

In Exercises 7–12, use the rank correlation coefficient to test for a correlation between the two variables. Use a significance level of α = 0.05.

Computers The following table lists quality rankings and costs (dollars) for different brands of laptop computers with 12 in. or 13 in. screens (based on data from Consumer Reports). Lower values of the quality rankings correspond to better computers. Do the more expensive brands appear to have better quality?

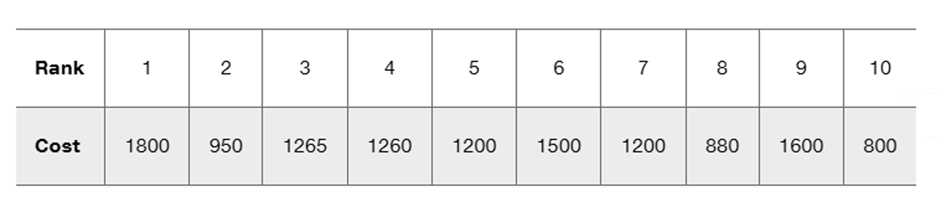
Table showing laptop quality ranks 1-10 with corresponding costs: 1800, 950, 1265, 1260, 1200, 1500, 1200, 880, 1600, 800.

Accepted Answer

Below there. Today we're gonna solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. The following table lists sound quality, rankings, and price. In dollars for different brands of wireless earbuds based on hypothetical data, lower values of the sound quality rankings correspond to better audio performance. In our far right column, we have our price in dollars, which represents why. Then in our middle column we have our sound quality rank denoted as X whereas price is denoted as Y. And finally in our far left column we have our brand and for our rows for the brand we have brand A, B, C, D, E, and F. And in order going across our row, starting with sound quality rank and then going to price for A we have 2 and 149, and then for B we have 5 and 99. For C we have 1 and 199, and for D we have 4 and 129. For E we have 3 and 139. And finally for F we have 6 and 79. Use the rank correlation coefficient to test for a correlation between the two variables. Use a significance level of alpha equals 0.05. Do the more expensive brands appear to have better sound quality? Fantastic. So it appears for this particular problem, we're trying to determine whether or not more expensive brands for earbuds appear to have better sound quality. So now that we know what we're ultimately trying to solve for, Our first step that we need to solve like first step we need to take in order to solve for this particular prompt, is we need to state our two different hypothesis values. So for our null hypothesis, we'll denote this as H0. We need to note that H0 or null hypothesis states that row is equal to 0. And for our alternative hypothesis, we'll say that H1 is what we're going to denote our alternative hypothesis. We could say that H1 states that row cannot equal 0. So once again for our null hypothesis, there is no correlation, whereas for our alternative alternative hypothesis, there is a correlation. So, now our first major step to solve for this particular problem is we need to assign the ranks and calculate our value for D2. So we're trying to find our value for D2. So, I've gone ahead. In order to help us solve for this problem more effectively, I've gone ahead and created a table for us to refer to to help us solve for this particular problem. And as you can see in our table, we have, going from our far left column, we have our brand, and then we have the sound quality rank, which we'll call RX. Then we have our price in units of dollars represented by Y. Then we have our rank price, which is denoted as RY. Then we have our value for DI is equal to R X minus R Y and then finally, our last column is our value for D subscript I to the power of 2. And as you could see. We going across row by row in order from A to F, we have 2, 149, 5, -3 and 9. And then we have for B 599 239, and then for C we have 1, 199, 65 and 25. For D we have 4, 129, 3, 11. And then for E, we got 3, 139, 4, -1 and 1. And finally, for F, we have 6, 79, 15, and 25, and then the sum of DI squared is 70. So essentially what we did is we took all of our known variables and we plugged it into our different formulas. So for DI equals RX minus RY we plugged in our value for RX and R Y and then we solved. And when we did, we received the following answers. So now, we also need to recall and note that the sum of D squad will be equal to 70. So now our third step is we need to calculate Spearman's rank correlation coefficient, which is the value of row. So we're trying to solve for row, and as we should recall, row is equal to 1 minus. 6 multiplied by the sum of D 2 all divided by n multiplied by parentheses n2 minus 1. And when we plug in our known variables, we will find that row is equal to 1 minus 6 multiplied by 70. Divided by 6 multiplied by 6 squared minus 1, and when we plug that into our calculator, we will find that row is simply equal to -1. So now our 4th step is we need to determine the critical value. So looking in our textbook and referring to Spearman's table, we will determine that the critical value using a two-tailed test will state that N is equal to 6, and we know that and once again N represents our sample size. So N equals 6, and alpha denotes our Significance, which is 0.05. So that will mean, once again, we're calling and using Spearman's table. Once again, this is a table that's in your textbook. We will find that this will give us a value that our critical value that is approximately equal to plus or minus 0. 886. Fantastic. So now, Our fifth and final step is we need to note that sense, row, or rather the absolute value of row is equal to 1, which is greater than 0.8. 86 we can reject the null hypothesis. So therefore, in conclusion, there is a significant negative rank correlation between price and quality rank or sound quality in this case. So therefore, as a result, more expensive brands tend to have lower rankings, which means that there will be better sound quality. So that will mean once again going up to look at our problem and to summarize what we've learned, that will mean that without a doubt our final answer has to be once again, yes, a strong negative rank correlation indicates that more expensive brands tend to have better sound quality and that's it. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

��app

Key Concepts

Rank Correlation Coefficient

Significance Level (α)

Hypothesis Testing

Watch next