8. Sampling Distributions & Confidence Intervals: Proportion
Confidence Intervals for Population Proportion
Struggling with Statistics?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
You wish to estimate with confidence the population proportion of people in Gen-Z that use social media. If you want your estimate to be accurate within of the population proportion, what is the minimum sample size needed?
A
422
B
423
C
405
D
406
Verified step by step guidance1
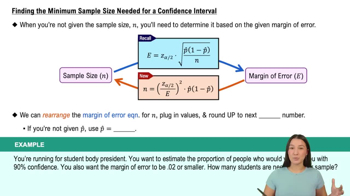
Identify the confidence level and margin of error: The confidence level is 90%, and the margin of error is 4% (0.04).
Determine the critical value (z-score) for a 90% confidence level. This can be found using a standard normal distribution table or calculator. The z-score for 90% confidence is approximately 1.645.
Use the formula for sample size estimation for a proportion: n = (z^2 * p * (1-p)) / E^2, where n is the sample size, z is the z-score, p is the estimated population proportion, and E is the margin of error.
Assume the most conservative estimate for the population proportion, p = 0.5, to ensure the maximum sample size. This is because the product p*(1-p) is maximized when p = 0.5.
Substitute the values into the formula: n = (1.645^2 * 0.5 * 0.5) / 0.04^2. Calculate the result to find the minimum sample size needed.
5:45mWatch next
Master Constructing Confidence Intervals for Proportions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
