Energy Consumption. Exercises 1–4 refer to the amounts of ener...

Question

Energy Consumption. Exercises 1–4 refer to the amounts of energy consumed in the author’s home. (Most of the data are real, but some are fabricated.) Each value represents energy consumed (kWh) in a two-month period. Let each subgroup consist of the six amounts within the same year. Data are available for download at www.TriolaStats.com.

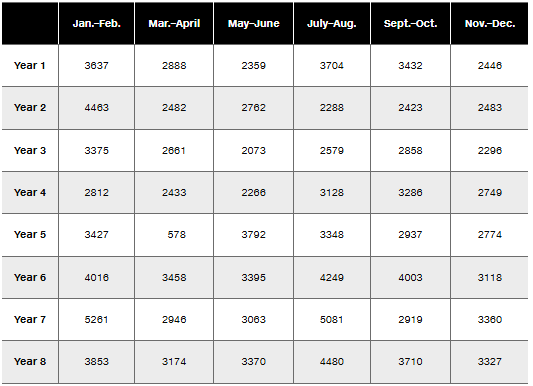
Table displaying energy consumption (kWh) data over eight years, organized by month and year.

Energy Consumption: R Chart Let each subgroup consist of the 6 values within a year. Construct an R chart and determine whether the process variation is within statistical control. If it is not, identify which of the three out-of-control criteria lead to rejection of statistically stable variation.

Accepted Answer

Hi, everyone. Let's take a look at this practice problem. This problem says the table below represents the range of energy consumption in kilowatt hours for each year over 5 years. Each row corresponds to a different year, and the range is calculated from the energy consumed across 6 2-month periods in that year. And below the text here, we're given a table, where in the first column, we have the year, and it has values of 1234, and 5. And in the last column, we have the range R and it has values of 1,345. 2,195, 1,302, 842, and 3,214. And we also have an average range of 1780. Let each year be a subgroup made up of the 6 values from that year. Create an R chart to determine whether the process variation is under statistical control. If not, determine which of the three out of control criteria produces a statistically unstable variation. And below this, we're given a blank graph on which to create our our chart. Now, in order to create our R chart, the first thing we want to do is to find our lower control limit and our upper control limit. So, we call for the lower control limit, which we'll label as LCL, that that is going to be equal to D3, multiplied by RR. Where our bar here is our average range. Now we can look up the value of the D3 in our standard statistical tables, but to do that, we'll need to determine the subgroup size N. And we're told in the problem. That each subgroup is made up of 6 values. That means that N is going to be equal to 6. So, looking up in our table, we see that with N equal to 6, that D3 is going to be equal to 0. So substituting in our values, we'll get our LCL is going to be equal to 0, multiplied by 1780. Which is equal to 0. Now, we'll do the same thing for upper control limit. UCL And this is going to be equal to D4, multiplied by R bar. And again, looking up our value for D4. We see that it has a value of 2.004. So that means our UCL. Is going to be equal to. 2.004. Multiplied by 1780. Which is going to be equal to. 3,567. And here we just rounded to the nearest whole number. So, we'll go ahead and plot these on our R chart. So, for the lower control limit, we'll place a dot. At 0 for each of our years. 1234, and 5, and then connect those 5 dots together. And this will give us our line or our lower control limit, which we'll label on the graph. As LCL. Then for our upper control limit, we will place a dot. At Each of our years at a value of 3,567. That'll be just slightly above the 3500 line. And then we'll just connect those 5 dots together to get our line for our upper control limit. And we will actually label that. As UCL. On our graph. And we can also plot. R mean our bar on the graph, and so that is going to occur at 1780. So again, we'll place a dot at 1780 for each of Or years? And then we'll just connect those dots to form a straight horizontal line. At that value, and we will label this. As Or bar And then finally, we actually have to plot our points. So, for year one, we have 1,345. So we'll place a point on the graph. At year one, at 1,345. For year two, we have 2,195. They will place a point. At that value on the graph above year 2. For year 3, we have a value of 1,302. The wolf place a point on the graph. Above your 3 at that value. For year 4, we have 842, so we'll place A dot on the graph at that value. And then for year 5, We have the value of 3,214. So we'll place a dot on the graph above your 5 for that value, and that we'll just connect our dots here. With straight lines In between each of these points. And once we've connected those dots, The resulting graph is going to be the answer for this problem. And if you look at a graph, We will see that the range that we plotted, Does not exceed the lower control limit or the upper control limit. So the process appears to be under statistical control. So that could be the answer to the second half of this problem. So I hope that this explanation has been useful, and I'll see you in the next video.

��app

Key Concepts

R Chart

Statistical Control

Out-of-Control Criteria

Watch next