In Exercises 1–5, refer to the following list of numbers of ye...

Question

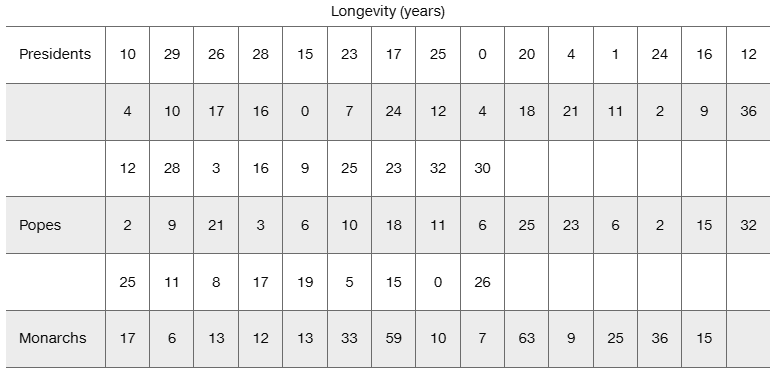
In Exercises 1–5, refer to the following list of numbers of years that deceased U.S. presidents, popes, and British monarchs lived after their inauguration, election, or coronation, respectively. (As of this writing, the last president is George H. W. Bush, the last pope is John Paul II, and the last British monarch is George VI.) Assume that the data are samples from larger populations.

[Image]

Exploring the Data Include appropriate units in all answers.

d. Are there any obvious outliers?

[Image]

Exploring the Data Include appropriate units in all answers.

d. Are there any obvious outliers?

Accepted Answer

Below there, today we're gonna solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. Refer to the following list of numbers of years that former CEOs of major technology companies lived after their official retirement. 1822, 1530, 1225 40, 1420 28 35 50. Identify any obvious outliers in the data set using the interquartile range IQR method. Awesome. So it appears for this particular prompt, we're ultimately trying to identify our final answer is we're trying to identify any obvious outliers in this particular data set that is provided to us by the prom itself, and we're asked to do this by using the interquartile range method or IQR for short. So we're trying to use the IQR method to solve for this particular problem. So with that said, let's read off our multiple choice answers to see what our final answer might be. A is yes, 40 and 50 are outliers. B is yes, 12 and 50 are outliers. C is no. There are no outliers in this data set, and D is yes, 50 is an outlier. Awesome. So first off, what we need to do in order to help us solve for this particular problem, we need to sort our data set into ascending order. So when we do that, we will get 1214, 15, 18, 202225, 28, 30, 35, 40 and 50. Awesome. So now our next step is we need to find the first quartile Q1 and the third quartile Q3. So let us quickly recall a note that Q1, so we'll call this Q1. Is the median of the lower half, so we need to take Q1, which once again is the median of the lower half, and Q1 is going to be equal to 15 + 18 divided by 2, which will be equal to when we round to one decimal place, 16.5. Let us also recall and note that Q3 is the median of the upper half, so that will mean that Q3 is equal to 30 + 35 divided by 2, which when we plug that into our calculator and round to one decial place, we will get 32.5. Fantastic. So now, our next step is we need to calculate the interquartile range, the IQR, so we need to calculate the IQR. And in order to do that, we should recall that the IQR, so this IQR value is going to be equal to Q3 minus Q1, which is going to be equal to 32.5 minus 16.5, which is going to be equal to simply 16, when we plug it into our calculator. So now, our next step is we need to determine the outlier boundaries. So focusing on the lower bound first, which I'll call LB for short, so the lower bound. So to determine the lower bound, we need to note that, as we should recall, Q1 minus 1.5 multiplied by the IQR is going to be equal to 16.5 minus parentheses 1.5 multiplied by 16, which when we plug it into our calculator is going to be. Simply equal to. 16.5, but we need to take 16.5, and we need to subtract 24, and when we do, we will find that this is equal to -7.5. And now focusing our attention on the upper bound, which I'll call UB for short. So the upper bound, which is going to be the equation for this, as we should recall, states that Q3. Plus 1.5 multiplied by our IQR value. So our IQR value. Plus So that's RTR. So now you have to add anything after that. So once again, we're focusing on the upper bound, so the upper bound equation, as we should recall, states that Q3 plus 1.5 multiplied by our IQR. Our IQR value, which is going to be equal to when we plug in our known values, 32.5 plus 1.5 multiplied by our IQR value, which is 16, which is going to be equal to, when we plug it into our calculator, 32.5, but we need to take 32.5 and we need to add 24. And when we do, we will find that it's equal to 56.5. So now we need to identify our outliers. So we need to recall and note that any values below negative 7.5 or above 56.5 are considered outliers. And since 50, since in our data set, the value of 50 is the highest value in our particular data set, it lies within our range, and because of that fact, there are no obvious outliers. And due to that fact, that means that our final answer, without a doubt has to be multiple choice answer letter C, which is no, there are no outliers in this data set. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

��app

Key Concepts

Outliers

Descriptive Statistics

Box Plot

Watch next