Finding Specified Data Values In Exercises 31–38, answer the q...

Question

Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.

Advanced Dental Admission Test The Advanced Dental Admission Test (ADAT) is designed so that the scores fit a normal distribution, as shown in the figure. (Source: American Dental Association)

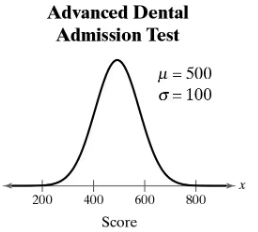
Graph of the Advanced Dental Admission Test scores showing a normal distribution with a mean of 500 and standard deviation of 100.

b. Between what two values does the middle 50% of the ADAT scores lie?

Accepted Answer

Hi everyone, let's take a look at this practice problem. This problem says a standardized language test has scores that follow a normal distribution with a mean U equal to 75 and a standard deviation stigma equal to 10. Determine the range of scores that include the middle 50% of all test takers. And we give four possible choices as our answers. For choice A, we have 67 to 84. For choice B, we have 65 to 81.ho C, we have 66 to 80, and for choice D, we have 68282. Now we need to determine the range of scores that include the middle 50% of all test takers. Now, the middle 50% of the distribution is between the 25th percentile and the 75th percentile, and these percentiles correspond to our first quartile, Q1 and third quartile Q3. So, we actually need to start off by finding the Z scores for these percentiles, and so we'll just be using our uh standard normal distribution table in order to find those values. So, for the 25th percentile, we'll be looking for the cumulative probability P of capital Z is less than Z25. And that is going to be equal to 25%, since we're at the 25th percentile, but we'll need that as a decimal, so dividing 25% by 100%, we'll get a value of 0.25%. And when we look up this value in our tables, we see that it corresponds to a Z value or Z25. That is going to be equal to minus 0.67. We'll do something similar for the 75th percentile. So, for its cumulative probability P of Z, which is less than Z75. And that is going to be equal to 0.75, since once we convert 75% to a decimal, we get 0.75. And again, we'll look this value up in our table, and we see that it corresponds to a Z value for Z75, that is going to be equal to 0.67. So now we have our two Z values here, we actually need to convert those back into test scores. And for this, we need to recall our formula 4 R Z score. I recall that our Z score, Z is equal to the quantity of X minus m in quantity divided by sigma. Where X here is gonna be our test score, mu is our mean, and sigma is our standard deviation. Now we're given our mean and standard deviation in the problem. And so, we know all the quantities, except for our X value. So, we're gonna start off by looking at the lower limit, which would correspond to the 25th percentile. So this will give us the lower test score on our range. So substituting in the values for Z will have Z25, which is minus 0.67, and that's going to be equal to X25. Minus from you, we're given a value on the problem of 75. And then we'll divide that quantity by sigma, which we're given that value in the problem as 10. So now we just need to solve this equation for X25, so the first thing we need to do is multiply both sides by 10 to get rid of the fraction. So we'll have minus 6.7 is equal to X25. -75. And to solve for X 25, we'll just need to add 75 to both sides. Doing so, we'll have that X25. It's going to be equal to 68, and here we just rounded to the nearest whole number. Now we have to do the same thing for our other Z score. So we'll look for X 75. So again, substituting in Z75 for a Z value will have 0.67, and that's going to be equal to the quantity of X 75 minus 75 in quantity divided by 10. So again, we need to solve this for X 75. So to do so, we'll again multiply by both sides by 10. To remove the fractions, we'll have 6.7. That's gonna be equal to X75 minus 75. And adding 75 to both sides will get that X 75 is going to be equal to 82. So it's gonna be the upper bound of our limit. And so that means for a final answer, that the range of scores that include the middle 50% of all test takers, is going to be 68. 282. So that is the final answer for this problem. And if we compare our answer to our answer choices, we see that the correct answer choice corresponds to answer choice D. So I hope that this explanation has been useful, and I'll see you in the next video.

��app

Key Concepts

Normal Distribution

Interquartile Range (IQR)

Z-scores

Watch next