Sketch a graph to represent the probability, then use a calculator to find it. 1.14\right)"> P ( Z > 1.14 ) P\left(Z>1.14\right) P ( Z > 1.14 )

Back, everyone. So let's take a look at this practice problem. Hopefully, you had a chance to solve it on your own. So we're gonna sketch your graph to represent this probability. We've got the probability that z is greater than 1.14. In other words, this is an area to the right problem. And then we're going to use our calculator in order to find that. Now I've got the list of steps here. Before you start plugging in a bunch of numbers in your calculator, I highly recommend that you just draw the graph out yourself. Always gonna think about this and visualize it yourself and then use your calculator to verify. Okay? That's what we're gonna do here. So I've got my center line. It's gonna be somewhere down over here. Again, this is an area to the right problem, so we're gonna shade all the area to the right. Our z score is 1.14. That's a positive number, so it's gonna be something somewhere over there. It doesn't have to be perfect, just a sketch. And, basically, because I'm dealing with an area to the right, I've got a greater than symbol, then the area that I'm actually gonna be calculating is gonna be this one over here, area to the right. Now what this means is if I were to try to use my z table, I'd have to look up this number, but then I have to subtract it because it's an area to the right. But we're gonna see how the calculator makes this much simpler. Okay? So we're gonna we're gonna see something like this in our calculator. Now let's go ahead and move on to the steps. So you're gonna go go ahead and hit that second VAR to get to the distribution, and then you're gonna go to the draw tab, and you're gonna hit the shade normal. Now, again, you could use normal CDF, plug in all the numbers, and it's just gonna give you a number. But I like to use the graph because it's more visual. Alright? So here's so that's the first step. Now now the next thing we're gonna do is we're actually gonna plug in our lower and upper bounds. Right? So, again, this is where you have to be careful here because depending on the problem, you're gonna plug in different things. So when we did an area to the left, we plugged in a lower of negative infinity and an upper of z. When we did between two values, we had to plug in different numbers. But it's actually neither of these 2. Right? It's not these. This is actually the kind of problem that we're dealing with, where z is greater than some number, 1.14. So it's actually kind of the opposite of what we did for the less than to the left, which is basically where instead of plugging in, negative infinity for the lower and then our upper, which is the z score we're interested in, we're actually gonna flip it. Our lower bound is gonna be the z score that we're interested in. Basically, you're telling the calculator, use this as your left boundary. And then your upper boundary is you're just gonna go all the way off until positive infinity. Right? So in other words, 1e99. So this is what we're gonna plug in for our numbers. So we're gonna plug in for our lower. This is gonna be 1.14, and then for the upper, it's gonna be 1e99. Okay. So we're gonna go over here, and we're for our lower, I'm gonna set this to 1.14. For upper, I'm gonna hit 1. And then if you can't figure out the e button, this is second, and it's right above the comma, right over here, this e, and then you're gonna hit 99. So remember, mu is 0, sigma is 1, nothing changes, and you're gonna hit the draw. So see how we got something that looks almost exactly like our sketched graph over here. This is why I love using this this feature. It makes it really difficult that you'll accidentally make a mistake. Okay? So we got something that lines up exactly with what we were expecting here, and I'm just gonna read off the value. So this value over here is gonna be an area of 0 points. So this is gonna be 0.0 oh, sorry. 1271. And I'll just keep it to 4 decimal places because that's what our z table showed. So in other words, this is the area that we would find. Now this is not the area that you would find in a z table because, remember, this, if you looked up this value right here, in a z table, it would tell you the area to the left, and then you'd have to subtract that, and then you end up finding it's this number. But this number represents essentially what's the area contained inside just that little shaded region. Okay? That's it for this one, folks. Hopefully, you got the right answer. Let me know if you have any questions. Thanks for watching.

Sketch a graph to represent the probability, then use a calculato...

6. Normal Distribution and Continuous Random Variables

Probabilities & Z-Scores w/ Graphing Calculator

Statistics

6. Normal Distribution and Continuous Random Variables

Probabilities & Z-Scores w/ Graphing Calculator

Struggling with Statistics?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

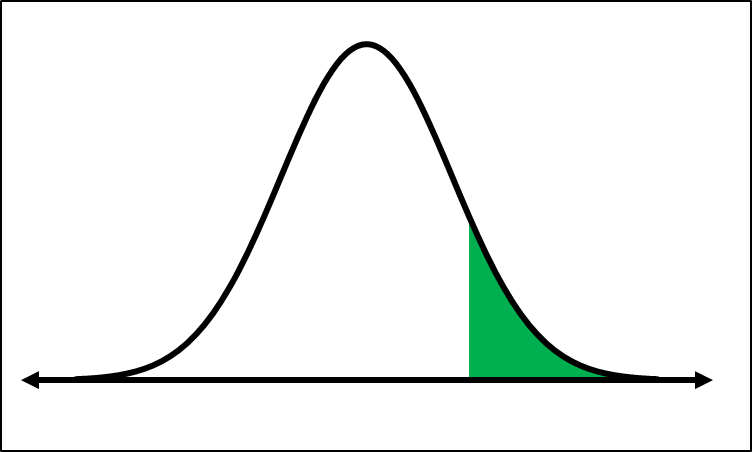
Sketch a graph to represent the probability, then use a calculator to find it.
$P\left(Z>1.14\right)$

0.1271

Graph showing the area under the normal distribution curve for P(Z > 1.14).

0.1271

Graph showing the area under the normal distribution curve for P(Z > 1.14) shaded in green.

0.8729

Graph showing the area under the normal distribution curve for P(Z > 1.14) shaded in green.

0.8729

Graph showing the area under the normal distribution curve for P(Z > 1.14).

Verified step by step guidance

Identify the problem as finding the probability that a standard normal variable Z is greater than 1.14, denoted as P(Z > 1.14).

Understand that the standard normal distribution is symmetric around zero, with a mean of 0 and a standard deviation of 1.

Sketch the standard normal distribution curve, which is bell-shaped, and shade the area to the right of Z = 1.14. This shaded area represents P(Z > 1.14).

Use a standard normal distribution table (Z-table) or a calculator with statistical functions to find the cumulative probability P(Z < 1.14).

Subtract the cumulative probability from 1 to find P(Z > 1.14), since the total area under the curve is 1. This gives you the probability of Z being greater than 1.14.

7:09m

Watch next

Master Probability From Given Z-Scores - TI-84 (CE) Calculator with a bite sized video explanation from Patrick

Start learning

����app

Struggling with Statistics?

Sketch a graph to represent the probability, then use a calculator to find it.P(Z>1.14)P\left(Z>1.14\right)P(Z>1.14)

Watch next

��app

Sketch a graph to represent the probability, then use a calculator to find it.
$P\left(Z>1.14\right)$