8. Sampling Distributions & Confidence Intervals: Proportion
Sampling Distribution of Sample Proportion
3:21 minutesProblem 6.5.1
Textbook Question
Satisfying Requirements Data Set 1 “Body Data” in Appendix B includes a sample of 147 pulse rates of randomly selected women. Does that sample satisfy the following requirement: (1) The sample appears to be from a normally distributed population; or (2) the sample has a size of n>30?
Verified step by step guidance1
Step 1: To determine if the sample appears to be from a normally distributed population, create a histogram or a normal probability plot of the pulse rates. A histogram should show a bell-shaped curve, and a normal probability plot should display points that closely follow a straight line.
Step 2: Perform a statistical test for normality, such as the Shapiro-Wilk test or the Kolmogorov-Smirnov test, using the pulse rate data. These tests provide a p-value to assess whether the data significantly deviates from a normal distribution.
Step 3: Evaluate the sample size condition. The problem states that the sample size is 147, which is greater than 30. This satisfies the requirement for n > 30.
Step 4: Combine the results from the normality assessment and the sample size evaluation. If the data is approximately normal or the sample size is sufficiently large (n > 30), the sample can be considered valid for statistical analysis.
Step 5: Document your findings clearly, noting whether the sample satisfies each requirement based on the analysis performed in the previous steps.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Normal Distribution
Normal distribution is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. In statistics, many tests and methods assume that the data follows a normal distribution, which is characterized by its bell-shaped curve. Understanding whether a sample is normally distributed is crucial for applying certain statistical techniques.
Recommended video:
Guided course
09:47
Finding Standard Normal Probabilities using z-Table
Sample Size and Central Limit Theorem
The Central Limit Theorem states that, for a sufficiently large sample size (typically n > 30), the sampling distribution of the sample mean will be approximately normally distributed, regardless of the shape of the population distribution. This theorem justifies the use of normal distribution methods for larger samples, making it essential to consider sample size when analyzing data.
Recommended video:
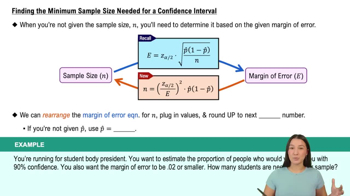
04:08Finding the Minimum Sample Size Needed for a Confidence Interval
Statistical Inference
Statistical inference involves using data from a sample to make conclusions about a larger population. It includes methods such as hypothesis testing and confidence intervals, which rely on the assumptions of normality and sample size. Understanding these concepts is vital for determining the validity of the conclusions drawn from the sample data.
Recommended video:
Guided course
05:53Parameters vs. Statistics
6:23mWatch next
Master Using the Normal Distribution to Approximate Binomial Probabilities with a bite sized video explanation from Patrick
Start learning
