Finding Specified Data Values In Exercises 31–38, answer the q...

Question

Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.

Water Footprint A water footprint is a measure of the appropriation of fresh water. The water footprint (in cubic meters) for a kilogram of wheat can be approximated by a normal distribution, as shown in the figure. (Source: Ecological Indicators)

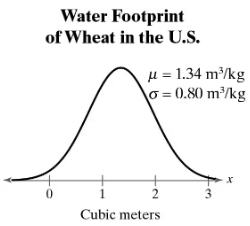
b. What water footprint represents the 29th percentile?

Accepted Answer

Hi, everyone. Let's take a look at this practice problem. This problem says in a certain region, the daily energy usage of households in kilowatt hours is normally distributed with a mean mu equal to 40 and a standard deviation sigma equal to 8. What daily energy usage represents the 29th percentile in this distribution? And we're given 4 possible choices as our answers. For choice A, we have 38.3 kilowatt hours. For choice B, we have 34.7 kilowatt hours. For choice C, we have 35.6 kilowatt hours, and for choice D, we have 39.1 kilowatt hours. So we need to find the daily energy usage that represents the 29th percentile in this distribution. Recall that the 29th percentile means that we're looking for the value of daily energy usage, such that 29% of the data lies to the left of it. So that means that the cumulative probability P of E is less than lowercase e is equal to 0.29. Where lowercase e here is the daily energy usage that we're looking for. Now, in order to find the value for that daily energy usage, we first want to find the corresponding Z score that corresponds to this cumulative probability. So, to find that Z score, we're gonna use our standard normal distribution tables. And in those tables, we'll look up the cumulative probability that is equal to 0.29. We see that the Z score that is closest to the value, it's going to be Z equal to minus 0.55. So we'll use a Z score in order to figure out our daily energy usage. And so here we call your relationship between a data value and the Z score. So in this case, our daily energy usage, which will have lowercase e, is going to be equal to, and here we call your formula. That's gonna be mu plus Z multiplied by sigma, where mu here is our mean and sigma is our standard deviation. We're given both of those quantities and the problem. That means that our daily energy usage is going to be equal to, for you, we're told the problem that we have a mean of 40, so we'll have 40. Plus, for Z value we will have minus 0.55. And that gets multiplied by our standard deviation sigma, which we're told the problem is 8. And when we evaluate this expression, we see that this is going to be Equal to 35.6. And this value is going to have units of kilowatt hours. And that's because both our mean and standard deviation have those units. So this here is the answer that we're looking for for this problem. And if we compare our answer here to our answer choices, we see that the correct answer choice corresponds to answer choice C. So, I hope this explanation has been useful, and I'll see you in the next video.

��app

Key Concepts

Normal Distribution

Percentiles

Z-scores

Watch next