Finding Critical Values Assume that we have two treatments (A ...

Question

Finding Critical Values Assume that we have two treatments (A and B) that produce quantitative results, and we have only two observations for treatment A and two observations for treatment B. We cannot use the Wilcoxon signed-ranks test given in this section because both sample sizes do not exceed 10.

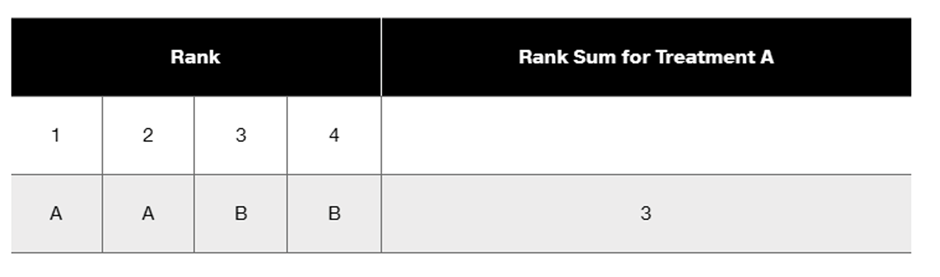
a. Complete the accompanying table by listing the five rows corresponding to the other five possible outcomes, and enter the corresponding rank sums for treatment A.

Table showing ranks 1-4 for treatments A and B, with rank sum for Treatment A as 3.

a. Complete the accompanying table by listing the five rows corresponding to the other five possible outcomes, and enter the corresponding rank sums for treatment A.

Accepted Answer

Hello there. Today we're going to solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. Suppose we have two treatments, X and Y. Each with only 2 quantitative observations because the sample sizes are small, fewer than 10, the Wilcoxen signed ranks test is not applicable. The combined data have been ranked from 1 lowest to 4 highest. Below is one possible assignment of treatments to ranks. So in our far right column, we have rank sum for treatment X, which totals 3, and then our other column to the to the left is 4, then our next column is 3, our next columns 2, next columns 1, and then our final column on the far left is for rank in our first call for our first row. So in our column, we have rank for 1 row, and then we have treatment assigned for our second row. And we have our ranks 123, and 4, and then we have our treatment assigned, which is X, X, Y, Y. So, rank 1 is X, ranks 2 is X, rank 3 is Y, and rank 4 is Y. And the rank sum for treatment X totals 3. So, which of the following is the correct list of all possible rank sums for treatment X when there are 2 values from treatment X and 2 from treatment Y ranked from 1 lowest to 4 highest? Awesome. So it appears for this particular prom, we're ultimately asked to figure out which of the following from our multiple choice list is the correct list for all possible rank sums for treatment X when there are two values. From treatment X and 2 from treatment Y ranked from 1 lowest to 4 highest. Awesome. So with that in mind, let's read off our multiple choice answers to see what our final answer set might be. A is 23467, B is 13579. C is 2347 and D is 34 567. Awesome. So first off, we select 2 ranks out of 4 to assign to treatment X. The remaining 2 will go to Y. So the number of such combinations in this particular case will be, so I'll write this as parentheses 4 C2. Where 4 C2, so this essentially means, as we should recall, let's make a note up above here. So this is saying that 4 factoral divided by parentheses 4 minus 2 in parentheses, multiplied by factoral, multiplied by 2 factoral is going to be equal to 6, so we could say that 4C2. is equal to 6, and Once again, we need to note, therefore, that there are 6 possible unique assignments of treatments to ranks. So considering this piece of information, if we were to collect all of our combinations and we can put them into a table, so our table, once again, this table that I have shared with you is a comb so once again, here are all the combinations and the corresponding rank sums. So we have our case on the far left column, which goes from 1 to 6, and then our next column is treatment assigned by rank, and then finally our far right column is the rank sum for treatment X. So for case one, the rank sum is 3, and then for 2 it's 4, for 3 it's 5, for 4, it's 5, for 5, it's 6, and for 6, it's 7. And as you can see for the treatment assignment by rank, we have X X Y Y and X gets ranks 1 and 2. And for case 2 going in numerical order to 6, we have X Y X Y. So X gets ranks 1 and 3, and then for 3, we got X, Y, YX where X gets ranks 1 and 4, and then for case 4. We have Y X X Y, where X gets ranks 2 and 3. For 5, we have Y, X, Y, X, where X gets ranks 2 and 4. And then finally for K 6 we have Y Y X X, where X gets ranks 3 and 4. So as you can see, therefore, the unique values of rank sums will be, without a doubt, 3,4,567. So that will mean looking at our multiple choice answers. Our correct answer without a doubt has to be multiple choice answer letter D, which once again is 3,4567. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

��app

Key Concepts

Rank Sums

Non-parametric Tests

Combinatorial Outcomes

Watch next