Car Colors
In Exercises 9–12, assume that 100 cars are r...

Question

Car Colors

In Exercises 9–12, assume that 100 cars are randomly selected. Refer to the accompanying graph, which shows the top car colors and the percentages of cars with those colors (based on PPG Industries).

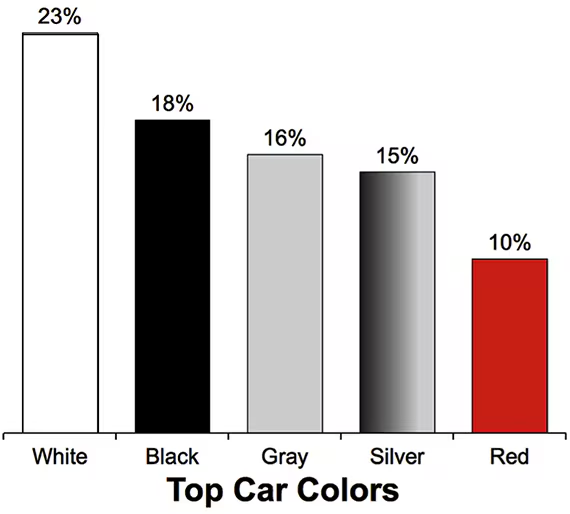
Bar graph showing top car colors: White 23%, Black 18%, Gray 16%, Silver 15%, Red 10%.

Black Cars Find the probability that at least 25 cars are black. Is 25 a significantly high number of black cars?

Accepted Answer

Hello. In this problem, we are told that in a large electronics store, a survey shows that the distribution of laptop colors sold are as follows 40% of laptops are silver, 30% are black, 15% are gray, 10% are blue, and 5% are other colors. Suppose 100 laptops are randomly selected from sale records. We want to find the probability that at least 35 laptops are black. Then we want to determine if 35 is a significantly high number of black laptops. So, let's go ahead and take a look at this phrase, which is at least 35 laptops. So, since we are trying to find the probability that from the sample size of 100, that 35 of them are at least black laptops, then that means that we are trying to find the probability. That the laptop that we pick is greater than equal to 35. Now, before we find this, let's just go ahead and list another piece of data. Since we are working with the random sample of 100 laptops, that means that we have a sample size N equal to 100. Furthermore, we're told that the probability P of the laptop being black is going to be 30%, or in other words, it'll be 0.3%. OK, so what we are dealing with is a binomial distribution. We are going to treat X as a binomial. Where we have a sample size of 100 and a probability of 0.3. So the first thing we need to do is we need to check the normal approximation. Now, for the normal approximation, we want to check the following. We want to check that the product Of our sample size and our probability are greater than equal to 5, and we want to check that the sample size multiplied by Q, which is the complement to the probability, is greater than or equal to 5. Now in this case here for the first one. Our sample size, multiplied by a probability, gives us 30, and 30 is greater than an equal to 5, so the first condition is met. Now, the complement of 30 is 70, so our sample size, multiplied by 0.7, is going to give us 70, which is greater than or equal to 5. So this satisfies the normal approximation, so we can assume that the data is normally distributed. Now what we want to do is we want to find the mean and standard deviation. Of the data set Now, in order to find the mean, the mean is defined as our sample size N multiplied by the probability, but we've already calculated this, it's going to be 30. So we just need to find our standard deviation. Now, standard deviation in the binomial distribution is defined as our sample size, multiplied by the probability, multiplied by the complement of the probability. This is going to be the square root of 100 multiplied by 0.3, multiplied by 0.7. And by plugging this into a calculator, we get 4.5826, which is our standard deviation. Now what we want to do is you want to check the continuity correction. Now for the continuity correction. We are able to translate the probability that X is greater than equal to 35, and set this equal to the probability that another variable Y, for example, is greater than equal to 35 minus 0.5. This will give us the probability that capital Y is greater than equal to 34.5. And now what we want to do is we want to translate this probability into a Z score. So the Z score is defined as the following. It is going to be 34.5 minus our mean divided by our standard deviation. That is going to be 34.5 minus 30, divided by 4.5826, and by plugging this into a calculator, we get the value of 0.98198. Now that we have the Z score, we can translate this this probability into a Z probability, and we get that we want to find the probability that Z is greater than or equal to 0.9. 981-98 Now, this is equivalent to 1 minus the probability that Z is less than 0.98198. And by using the Z table, we are able to translate this probability. And we get The following value We get that the probability that Z is greater than 0.98198 is 0.1635. And this is going to be the probability that the computers are black. And since 0.6 0.1634, What the hell?

��app

Key Concepts

Probability

Binomial Distribution

Statistical Significance

Watch next