In Exercises 5–8, identify the class width, class midpoints, a...

Question

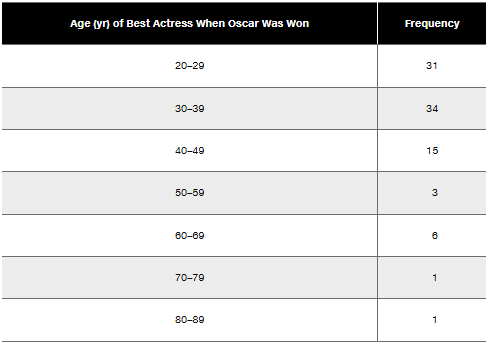
In Exercises 5–8, identify the class width, class midpoints, and class boundaries for the given frequency distribution. Also identify the number of individuals included in the summary. The frequency distributions are based on real data from Appendix B.

Table displaying age ranges of best actresses when they won Oscars, along with corresponding frequency counts.

Accepted Answer

All right, hello, everyone. So this question says lifespan of pet dogs. The table below summarizes the lifespan of pet dogs in a study. Identify the class with, class midpoints, and class boundaries for the given frequency distribution. Also, determine the total number of dogs included in the summary. So first, let's begin with finding the class width. Now, what I did here towards the bottom of the screen is make a table with the data points that we need to calculate, as well as the classes that were already given to us in the original chart. So recall that in order to find the class with, what you do is subtract the lower boundary of one class from the lower boundary of the next one. So, when you consider the first two classes, for example, that is 2 to 9 and 10 to 17 years, you would subtract the lower boundaries of 10 and 2 to give you 8. So the class width is going to be 8. And that just so happens to be the case for all of the classes given, so I'm just going to write that out. From here you find the class midpoints. Now, the class midpoint is found by first taking the sum of the lower boundary and upper boundary of that class, and then dividing that sum by 2. So using the first class as an example once again. The upper and lower boundaries, or rather, lower and upper boundaries respectively, are 2 and 9. So the sum of 2 and 9, 11, divided by 2, gives you the midpoint of 5.5. And then you would repeat this calculation for the remaining classes. So for the second class, that would be 13.5. For the third, that would be 21.5. For the 4th that'll be 29.5. For the 5th 37.5. For the 6 45.5. And for the 7th, 53.5. So now how do you find the class boundaries? Well, recall it class boundaries ensure that there are no gaps in between consecutive intervals. So Here When you take the lower boundary of a given class. Or the lower limit of a given class, the lower class boundary is taken by subtracting 0.5 from that lower limit. So going back to the first class once again, ranging from 2 to 9 years, when you take that lower limit of 2 and subtract 0.5, you obtain the lower class boundary of 1.5. Additionally, you would take the upper limit of each class, in this case 9 in our example, and add 0.5 to it to obtain the upper class boundary. So for the first one, that would be 9.5. So now, you would repeat the calculations as demonstrated before. The class boundaries for the second class would be then 9.5 up to 17.5. For the third, that's 17.5 up to 25.5. For the 4th that would be 25.5. Up to 33.5. For the 5th, that would be 33.5. Up to 41.5. For the 6th, that would be 41.5 up to 49.5. And for the last one that would be. 49.5 up to 57.5. So now that our table has been filled out, our last step is to find the total number of dogs. And in this case, because we're given a frequency distribution, to find the total number of dogs included in the summary, what you do is add all the frequencies. So going back to our original data. You would add 28, 36, 12, 452, and 1. And that Gives you, of course, the total number. Which happens to be 88. And that completes your final answer. So with that being said, thank you so very much for watching and I hope you found this helpful.