4. Probability
Basic Concepts of Probability
2:48 minutesProblem 3.1.68
Textbook Question
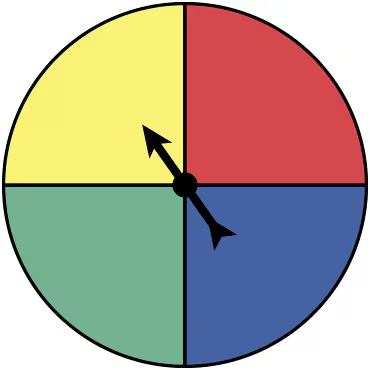
Using a Tree Diagram In Exercises 67-70, a probability experiment consists of rolling a six-sided die and spinning the spinner shown at the left. The spinner is equally likely to land on each color. Use a tree diagram to find the probability of the event. Then explain whether the event can be considered unusual.
68. Event B: rolling an odd number and the spinner landing on green
Verified step by step guidance1
Step 1: Understand the problem. The experiment involves rolling a six-sided die and spinning a spinner with four equally likely colors: yellow, red, green, and blue. Event B is defined as rolling an odd number and the spinner landing on green.
Step 2: Identify the outcomes for rolling the die. A six-sided die has outcomes {1, 2, 3, 4, 5, 6}. Odd numbers are {1, 3, 5}, so there are 3 favorable outcomes for rolling an odd number.
Step 3: Identify the outcomes for the spinner. The spinner has 4 equally likely outcomes: yellow, red, green, and blue. The favorable outcome for Event B is the spinner landing on green, which is 1 out of 4 outcomes.
Step 4: Use a tree diagram to represent the combined outcomes. For each roll of the die (1, 2, 3, 4, 5, 6), draw branches for each spinner outcome (yellow, red, green, blue). Highlight the branches where the die roll is odd (1, 3, 5) and the spinner lands on green.
Step 5: Calculate the probability of Event B. Multiply the probability of rolling an odd number (3/6) by the probability of the spinner landing on green (1/4). This gives the probability of Event B. To determine if the event is unusual, compare the probability to a threshold (e.g., less than 0.05 is considered unusual).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
5:37mWatch next
Master Introduction to Probability with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
