Finding Standard Deviation from a Frequency Distribution. In E...

Question

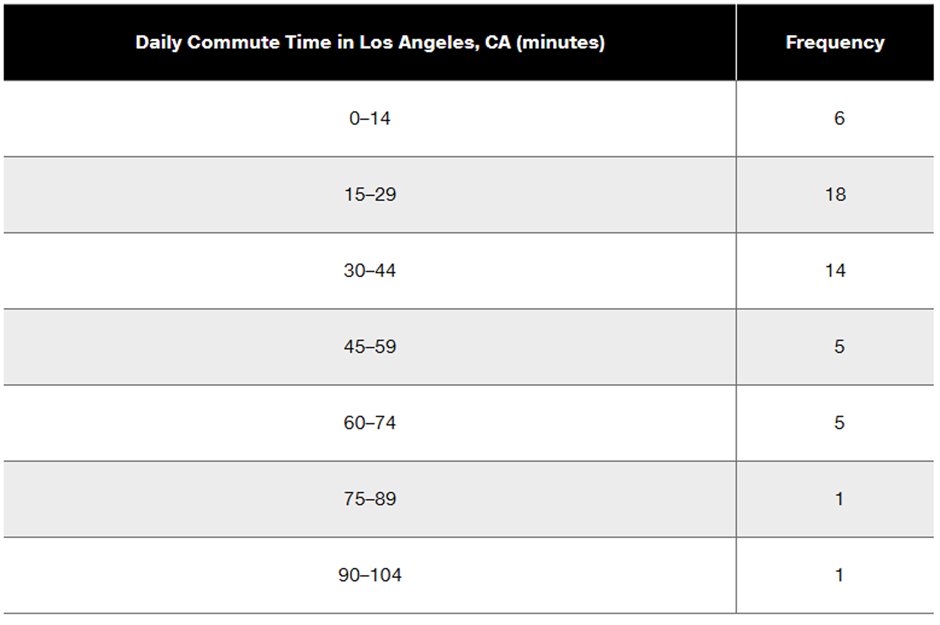
Finding Standard Deviation from a Frequency Distribution. In Exercises 37–40, refer to the frequency distribution in the given exercise and compute the standard deviation by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviations to these standard deviations obtained by using Formula 3-4 with the original list of data values: (Exercise 37) 18.5 minutes; (Exercise 38) 36.7 minutes; (Exercise 39) 6.9 years; (Exercise 40) 20.4 seconds.

Standard deviation for frequency distribution

Standard deviation for frequency distribution

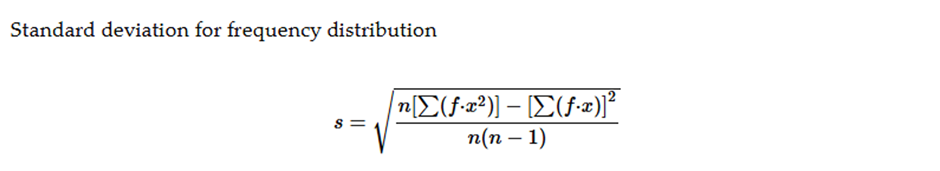
Standard deviation formula for frequency distribution, showing variables n, f, and x.

Table showing daily commute times in Los Angeles, CA, with frequency counts for each time interval in minutes.

Accepted Answer

Welcome back, everyone. Using the frequency distribution provided below, calculate the standard deviation using the given formula where X denotes the class midpoint, F is the class frequency, and N represents the total number of sample values. The formula says that the standard deviation is equal to the square root of N multiplied by the sum of frequency multiplied by X2. Minus the sum of the frequency f multiplied by X all squared divided by n multiplied by n minus 1. After we do that, we want to compare our calculated standard deviation with the value of 12.55 obtained using the sum of squares of deviations formula. For our answer choices, A says the standard deviation from the frequency distribution is identical to the standard deviation from the original data. B says it's slightly lower than the one from the original data due to class grouping. C says it's significantly different, suggesting a loss of accuracy in grouping, and the D says it's completely unreliable compared to the other. Now, let's first find the some the the standard deviation using our formula. OK? So we have our class intervals, frequencies, and we'll need to find the values of X. Those are the class midpoints. And we'd also need to figure out then what F multiplied by X curd would be, if multiplied by X would be, and then some those values so that we can plug it into our formula. So let's make a table, OK? And in our table, we are going to have our class, OK. Let me, let me put a line here actually. So, we're gonna have our class interval. We're going to have our midpoints, OK? We are going to have our value of, well, after we have our midpoint, then we're gonna have a value of our frequency, OK? And then we're gonna multiply our frequency F by our midpoint X and then multiply our frequency F by X2. OK? So, these are all the values that we need. So let me extend here yeah. And let's just, let's just do a nice little table that makes it a bit easier to work with, OK? No, of course, I should put here that our midpoint is X. Think I can make this table a bit shorter at the end. So what do we know? Well, we know that we have 5 classes, OK. We, we go from 10 to 1920 to 29. 30 to 39, 40 to 49, and 50 to 59. And from the table that we are already given, we know that the frequencies are 58, 1215 and 10, respectively, OK? So now we need to fill in all of these values. Let's first start with the midpoint, OK? What do we know about the midpoint? Well, recall that the midpoint is going to be equal to the lower bound. Yeah. Plus the upper bound. All divided by 2 for each class, OK, so for example here. For a midpoint between 10 to 19, it's going to be the lower bone 9.5 plus the upper bone 19.5. OK, all divided by 2. And now, in that case that would be 29 divided by 2, which would equal 14.5. In that and and we just repeat the same idea for the rest of the midpoints. Now if midpoint for 10 to 19 is 14.5, for 20 to 29, it's 24.5, 30 to 39, 34.5, 40 to 49, 44.5, and 50 to 59 is 54.5. Know that we have the midpoint and the frequencies, we can find their product. For example, for the class 10 to 19, F multiplied by X would be 5 multiplied by 14.5, which is 72.5. On the other hand, for 20 to 29, it would be 24.5 multiplied by 8, which is 196, uh, 30 to 39, 34.5 multiplied by 12, 414, 40 to 49, 44.5 multiplied by 15, which is 667.5, and 50 to 59 would be 54.5 multiplied by 10 or 545. OK? Now that we have those values, next we can find the value of XF multiplied by X square. No, in this case, then it would be, for example, the class 10 to 19, the 5 multiplied by 72, OK, or sorry, it would be 5 multiplied by 14.5 squared, OK? And when we do that. OK, when we do that, we're going to get 1,0051.25. So our frequency multiplied by X2. If we do that for the rest of our values, for 20 to 29, it would be 8 multiplied by 24.5 squared, which is 4,802. For 30 to 39, it would be 12 multiplied by 34.5 squared, which is 14,283. For 40 to 49, it's 15 multiplied by 44.5 squared, which is 29,703.75 and finally for interval of 50 to 59, it would be 10 multiplied by 54.5 squared, which is 29,702.5. Now that we have F multiplied by X and F multiplied by X2, we can sum them. OK, so let me get rid of my formula here. And no, that means in total, if we start to add everything up, OK. Then we know that our total frequency, the sample size N, is going to be 50. OK. Uh, the sum of F multiplied by X. Is going to be equal to 1,895. And the sum of F multiplied by X squared is 79,542.5. No, we have everything we need to find the standard deviation using the frequency distribution because by substituting the valid in the formula we're going to get N50 multiplied by the sum of multiplied by X2 7979,542.5 minus the sum of F multiplied by XR squared, so that's 1,895 squared. All divided by N50 multiplied by N minus 1, 50 minus 1. I know if we go ahead and calculate here, we get our standard deviation to be 12.55. Now remember earlier. We knew that in our problem the standard deviation of 12.55 was also obtained using the sum of squares of deviations formula. So what does that tell us? Well, no, we can conclude that the standard deviation from the frequency distribution is identical to the standard deviation from the original data. Therefore, A is the correct answer. Thanks a lot for watching everyone. I hope this video helped.

��app

Watch next

����app

Watch next

��app