You want to make a 97 % 97\% confidence interval for the population proportion of people between 20 − 30 20-30 years old who have gotten a speeding ticket in the past 2 2 years. A prior study found that 26 % 26\% of people between 20 − 30 20-30 years old have received a speeding ticket in the last year. If you want your estimate to be accurate within 3 % 3\% of the true population proportion, what is the minimum sample size needed?

wanna make a 97% confidence interval for the population proportion of people between 20 to 30 years old who've gotten a speeding ticket in the past 2 years. Now, a prior study found that 26% of people between those ages have received a speeding ticket in those last 2 years. If you want your estimate to be accurate within 3% of the true population proportion, what is the minimum sample size needed? So in this particular problem, we are given our margin of error, e, as 3%, which is 0.03, and we're also given p hat. That's that 0.26 because it's 26%. Now the only other thing that we need here in order to find that minimum sample size is our critical z score. Because we have a confidence level of 97%, we can take alpha over 2. That's equal to 1 minus that 0.97 over 2, which is 0.015. This then corresponds to a critical z score, z alpha over 2 of 2.17. So now we have everything we need here in order to find that minimum sample size. Remember n that sample size is going to be equal to z alpha over 2 over e. That whole term gets squared. And then this is multiplied by P hat times 1 minus P hat. Plugging all of our values in here, that's going to be 2.17 over 0.03. Squaring that term, multiplying it by 0.26, that's p hat, then 1 minus 0.26 is 0.74. Now multiplying this out here gives us a value of 1,006 point 66. But remember, we cannot take 0.66 of a sample, so we need to go ahead and round that up to the next whole number. And the minimum sample size needed here is 1,007 people. Feel free to let us know if you have any questions, and we'll see you in the next one.

You want to make a 97%97\% confidence interval for the population...

8. Sampling Distributions & Confidence Intervals: Proportion

Confidence Intervals for Population Proportion

Statistics

8. Sampling Distributions & Confidence Intervals: Proportion

Confidence Intervals for Population Proportion

Struggling with Statistics?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

You want to make a $97 percent sign$ confidence interval for the population proportion of people between $20 minus 30$ years old who have gotten a speeding ticket in the past $2$ years. A prior study found that $26 percent sign$ of people between $20 minus 30$ years old have received a speeding ticket in the last year. If you want your estimate to be accurate within $3 percent sign$ of the true population proportion, what is the minimum sample size needed?

1007

1006

579

1309

Verified step by step guidance

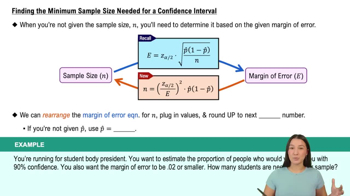
Identify the key components needed for calculating the sample size for a confidence interval for a population proportion. These include the desired confidence level, the margin of error, and an estimate of the population proportion.

For a 97% confidence interval, determine the z-score associated with this confidence level. The z-score is a critical value that corresponds to the desired level of confidence. For a 97% confidence level, the z-score is approximately 2.17.

Use the formula for the sample size of a population proportion: n = (z^2 * p * (1-p)) / E^2, where n is the sample size, z is the z-score, p is the estimated population proportion, and E is the margin of error.

Substitute the known values into the formula: z = 2.17, p = 0.26 (from the prior study), and E = 0.03 (the desired margin of error).

Calculate the sample size using the formula. Ensure that the result is rounded up to the nearest whole number, as the sample size must be a whole number.

5:45m

Watch next

Master Constructing Confidence Intervals for Proportions with a bite sized video explanation from Patrick

Start learning

����app

Struggling with Statistics?

Watch next

��app