6. Normal Distribution and Continuous Random Variables
Standard Normal Distribution
2:27 minutesProblem 5.1.45
Textbook Question
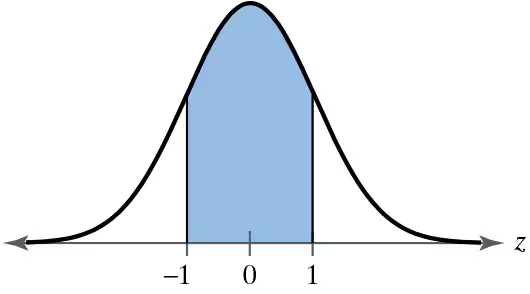
Finding Probability In Exercises 41–46, find the probability of z occurring in the shaded region of the standard normal distribution. If convenient, use technology to find the probability.
Verified step by step guidance1
Step 1: Identify the problem. The question asks for the probability of z occurring in the shaded region of the standard normal distribution. From the image, the shaded region lies between z = -1 and z = 1.
Step 2: Understand the standard normal distribution. It is a bell-shaped curve with a mean of 0 and a standard deviation of 1. Probabilities are calculated using the area under the curve.
Step 3: Use the z-scores provided (-1 and 1) to find the cumulative probabilities. The cumulative probability for a z-score represents the area under the curve to the left of that z-score.
Step 4: To find the probability of z occurring in the shaded region, calculate the cumulative probability for z = 1 and subtract the cumulative probability for z = -1. This gives the area between these two z-scores.
Step 5: If convenient, use technology (such as a graphing calculator, statistical software, or online tools) to find the cumulative probabilities for z = -1 and z = 1. Subtract the smaller cumulative probability from the larger one to determine the probability of z occurring in the shaded region.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Standard Normal Distribution
The standard normal distribution is a special case of the normal distribution where the mean is 0 and the standard deviation is 1. It is represented by the bell-shaped curve, which is symmetric about the mean. This distribution is crucial for calculating probabilities associated with z-scores, which indicate how many standard deviations an element is from the mean.
Recommended video:
Guided course
09:47
Finding Standard Normal Probabilities using z-Table
Z-scores
A z-score is a statistical measurement that describes a value's relationship to the mean of a group of values. It is calculated by subtracting the mean from the value and then dividing by the standard deviation. Z-scores allow for the comparison of scores from different distributions and are essential for finding probabilities in the standard normal distribution.
Recommended video:
Guided course
06:31Z-Scores From Given Probability - TI-84 (CE) Calculator
Probability Area
The probability area under the curve of the standard normal distribution represents the likelihood of a random variable falling within a specific range of values. In the context of z-scores, the shaded region between two z-scores indicates the probability of a value falling between those scores. This area can be calculated using statistical tables or technology, such as calculators or software.
Recommended video:
5:37Introduction to Probability
9:47mWatch next
Master Finding Standard Normal Probabilities using z-Table with a bite sized video explanation from Patrick
Start learning
