4. Probability
Complements
2:18 minutesProblem 5.q.7
Textbook Question
In Exercises 6–10, refer to the accompanying table, which describes the numbers of adults in groups of five who reported sleepwalking (based on data from “Prevalence and Comorbidity of Nocturnal Wandering In the U.S. Adult General Population,” by Ohayon et al., Neurology, Vol. 78, No. 20).
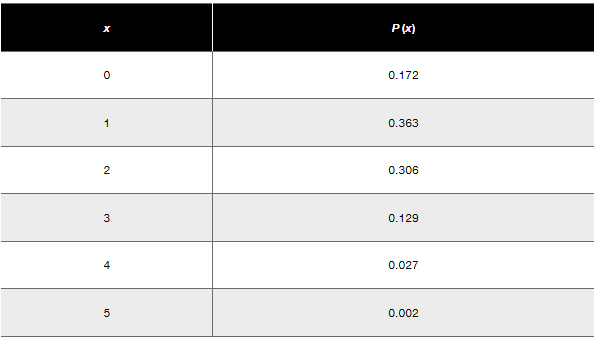
Probability Find the probability that at least one of the subjects is a sleepwalker.
Verified step by step guidance1
Step 1: Understand the problem. The goal is to find the probability that at least one of the subjects is a sleepwalker. This can be calculated using the complement rule, which states that the probability of 'at least one' is equal to 1 minus the probability of 'none'.
Step 2: Identify the probability of 'none' from the table. The table provides the probability P(x) for different values of x, where x represents the number of sleepwalkers. For x = 0 (no sleepwalkers), P(0) = 0.172.
Step 3: Apply the complement rule. The formula for the probability of at least one sleepwalker is: P(at least one) = 1 - P(none). Substitute the value of P(none) from the table into this formula.
Step 4: Perform the subtraction. Subtract the probability of 'none' (P(0) = 0.172) from 1 to find the probability of at least one sleepwalker.
Step 5: Interpret the result. The resulting probability represents the likelihood that at least one of the five subjects is a sleepwalker based on the given data.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Probability
Probability is a measure of the likelihood that a particular event will occur, expressed as a number between 0 and 1. In this context, it quantifies the chance of sleepwalking occurrences among a group of five adults. The sum of probabilities for all possible outcomes must equal 1, allowing for the calculation of probabilities for specific events, such as at least one sleepwalker.
Recommended video:
5:37
Introduction to Probability
Complement Rule
The complement rule in probability states that the probability of an event occurring is equal to 1 minus the probability of it not occurring. For this question, to find the probability that at least one subject is a sleepwalker, one can calculate the probability that none are sleepwalkers and subtract it from 1. This simplifies the calculation and provides a clearer understanding of the event's likelihood.
Recommended video:
4:23Complementary Events
Discrete Probability Distribution
A discrete probability distribution describes the probabilities of the possible values of a discrete random variable. In the provided table, the variable x represents the number of sleepwalkers in a group of five, and P(x) gives the probability of each outcome. Understanding this distribution is essential for analyzing the likelihood of different scenarios, such as determining the probability of at least one sleepwalker.
Recommended video:
Guided course
04:48Variance & Standard Deviation of Discrete Random Variables
4:23mWatch next
Master Complementary Events with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice