Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
Graphing Exponential Functions
Struggling with College Algebra?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Graph the given function.
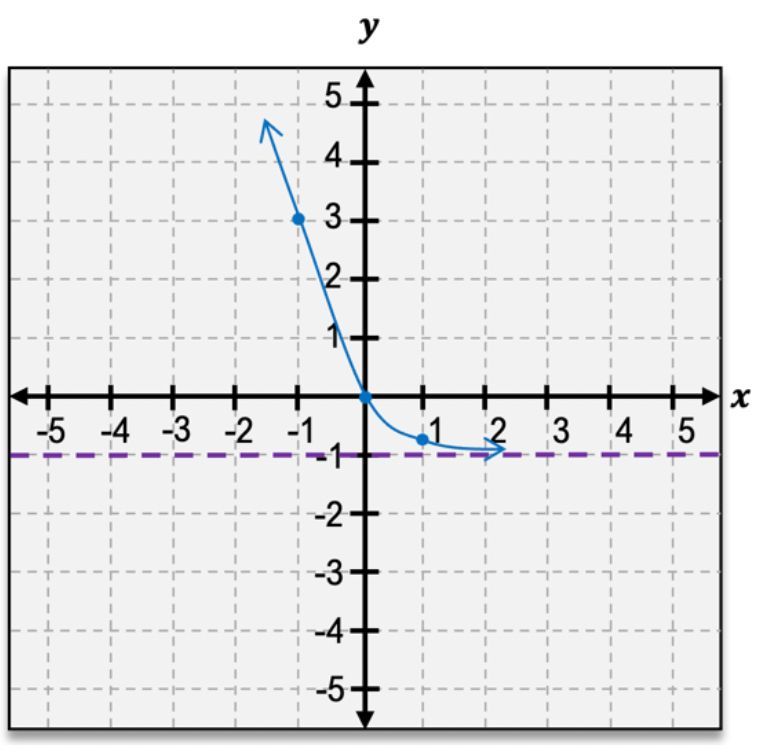
g(x)=4ŌłÆxŌłÆ1
A
B
C
D
 Verified step by step guidance
Verified step by step guidance1
Identify the function type: The given function is an exponential function of the form g(x) = 4^{-x} - 1.
Determine the horizontal asymptote: For the function g(x) = 4^{-x} - 1, the horizontal asymptote is y = -1.
Find the y-intercept: Set x = 0 in the function to find the y-intercept. g(0) = 4^{0} - 1 = 1 - 1 = 0, so the y-intercept is (0, 0).
Analyze the behavior of the function: As x approaches positive infinity, 4^{-x} approaches 0, so g(x) approaches -1. As x approaches negative infinity, 4^{-x} becomes very large, so g(x) becomes very large.
Plot key points and asymptote: Plot the y-intercept (0, 0) and the horizontal asymptote y = -1. Sketch the curve starting from the y-intercept, approaching the asymptote as x increases, and rising steeply as x decreases.

 5:46m
5:46mWatch next
Master Graphs of Exponential Functions with a bite sized video explanation from Patrick
Start learning