4. Probability
Addition Rule
2:55 minutesProblem 3.Q.2e
Textbook Question
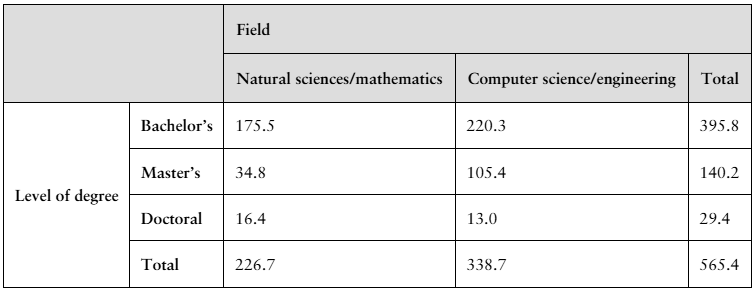
The table shows the numbers (in thousands) of earned degrees by level in two different fields, conferred in the United States in a recent year. (Source: U.S. National Center for Education Statistics)
A person who earned a degree in the year is randomly selected. Find the probability that the degree earned by the person is a
g. bachelor's degree and the degree is in natural sciences/mathematics.
Verified step by step guidance1
Step 1: Identify the relevant data from the table. The number of bachelor's degrees in natural sciences/mathematics is 175.5 (in thousands), and the total number of degrees conferred across all fields and levels is 565.4 (in thousands).
Step 2: Recall the formula for probability. The probability of an event is calculated as the ratio of the number of favorable outcomes to the total number of outcomes. In this case, the favorable outcome is earning a bachelor's degree in natural sciences/mathematics.
Step 3: Write the probability formula for this scenario: \( P = \frac{\text{Number of bachelor's degrees in natural sciences/mathematics}}{\text{Total number of degrees}} \). Using MathML, this can be expressed as:
Step 4: Simplify the fraction to calculate the probability. This involves dividing the numerator (175.5) by the denominator (565.4).
Step 5: Interpret the result. The probability represents the likelihood that a randomly selected person who earned a degree in the year obtained a bachelor's degree in natural sciences/mathematics.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Probability
Probability is a measure of the likelihood that a particular event will occur, expressed as a number between 0 and 1. In this context, it refers to the chance of randomly selecting a person who earned a bachelor's degree in natural sciences/mathematics from the total number of degrees conferred. Understanding how to calculate probability is essential for answering the question accurately.
Recommended video:
5:37
Introduction to Probability
Total Counts
Total counts refer to the sum of all occurrences of a particular category within a dataset. In the table, the total number of degrees conferred in each field and level of degree is crucial for determining the overall probability. For instance, the total number of bachelor's degrees is necessary to find the probability of selecting a bachelor's degree in natural sciences/mathematics.
Recommended video:
04:04Fundamental Counting Principle
Conditional Probability
Conditional probability is the probability of an event occurring given that another event has already occurred. In this scenario, we are interested in the probability of selecting a bachelor's degree in natural sciences/mathematics, which is a specific condition within the broader context of all degrees. This concept helps in understanding how to narrow down the sample space when calculating probabilities.
Recommended video:
5:37Introduction to Probability
5:14mWatch next
Master Probability of Mutually Exclusive Events with a bite sized video explanation from Patrick
Start learning
