Identifying Probability Distributions In Exercises 27 and 28, det...

Table of contents

Skip topic navigation

1. Intro to Stats and Collecting Data55m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically1h 45m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables2h 33m
6. Normal Distribution and Continuous Random Variables1h 38m
7. Sampling Distributions & Confidence Intervals: Mean1h 3m
- Introduction to Confidence Intervals
  15m
- Confidence Intervals for Population Mean
  48m
8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- Sampling Distribution of Sample Proportion
  29m
- Confidence Intervals for Population Proportion
  42m
9. Hypothesis Testing for One Sample1h 1m
- Steps in Hypothesis Testing
  1h 1m
10. Hypothesis Testing for Two Samples2h 8m
11. Correlation48m
- Scatterplots & Intro to Correlation
  26m
- Correlation Coefficient
  21m
12. Regression1h 4m
13. Chi-Square Tests & Goodness of Fit1h 20m
14. ANOVA1h 0m

5. Binomial Distribution & Discrete Random Variables

Discrete Random Variables

Statistics

5. Binomial Distribution & Discrete Random Variables

Discrete Random Variables

Previous problemNext problem

2:25 minutes

Problem 4.1.27

Textbook Question

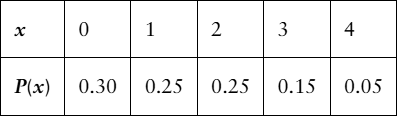
Identifying Probability Distributions In Exercises 27 and 28, determine whether the distribution is a probability distribution. If it is not a probability distribution, explain why.

Verified step by step guidance

Step 1: Understand the requirements for a probability distribution. A probability distribution must satisfy two conditions: (1) The sum of all probabilities must equal 1, and (2) each individual probability must be between 0 and 1 inclusive.

Step 2: Verify the first condition by summing all the probabilities in the table. Add P(0), P(1), P(2), P(3), and P(4). Use the formula: \( \sum P(x) = P(0) + P(1) + P(2) + P(3) + P(4) \).

Step 3: Check the second condition by ensuring that each probability value in the table (0.30, 0.25, 0.25, 0.15, 0.05) is between 0 and 1 inclusive. If any value is outside this range, the distribution is not valid.

Step 4: If both conditions are satisfied, conclude that the given distribution is a probability distribution. If either condition fails, explain why the distribution is not valid.

Step 5: Interpret the results and provide reasoning based on the checks performed in steps 2 and 3. For example, if the sum of probabilities is not equal to 1, state the discrepancy and its impact on validity.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Probability Distribution

A probability distribution describes how probabilities are assigned to each possible value of a random variable. For a distribution to be valid, the probabilities must be non-negative and sum to one. This concept is fundamental in statistics as it provides a framework for understanding the likelihood of different outcomes.

Sum of Probabilities

In a valid probability distribution, the sum of all probabilities must equal 1. This ensures that the total likelihood of all possible outcomes is accounted for. If the sum is less than or greater than 1, the distribution cannot be considered valid, indicating an error in the assignment of probabilities.

Non-negativity of Probabilities

Probabilities must be non-negative, meaning they cannot be less than zero. This principle is essential because negative probabilities do not have a meaningful interpretation in the context of likelihood. Each probability value in a distribution must reflect a real chance of occurrence, reinforcing the need for non-negativity.

Watch next

Master Intro to Random Variables & Probability Distributions with a bite sized video explanation from Patrick

Start learning

����app